Algebra- A három szabálya
A három egyszerű szabálya az arányosság meghatározásának módszere.
A harmad egyszerű szabálya egy olyan matematikai módszer, amely lehetővé teszi, hogy az arányossági egyenlet egyik tagját a többi alapján határozzuk meg.
A szabály visszatér a negyedik arányszám kiszámításához az arányokból:
a/b=c/x - Számítsa ki a százalékot % A százalékok kiszámítása
Mennyi X %-a az Y számnak?
Hogyan lehet kiszámítani egy szám százalékát?
A három egyszerű szabály is használható - Számtani átlaga
Képlet
ma = (x1+x2+ ... + xn) / n
Ha a,b és c valós számok, akkor a számtani átlaguk ma = (a+b+c) / 3 - Törtek tizedesjegyben – hogyan tudom megtenni?
Minden 10-es nevezőhatékonyságú közönséges tört felírható tizedes törtként.
Hogyan alakíthatok át egy törtet decimális számmá?
Tanulja meg, hogyan írjon közönséges törteket tizedes formában.
Hogyan konvertálhatok decimálisról binárisra?
Geometria a térben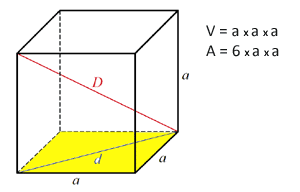 A kocka térfogata A kocka térfogata
Hogyan kell kiszámítani a kocka térfogatát?
Mi a képlet és az ábra.
A térfogat egyenlő az alapterület és a magasság szorzatával (négyzetes oldal szorozva a - a2*a-val)
V = a*a*a = a3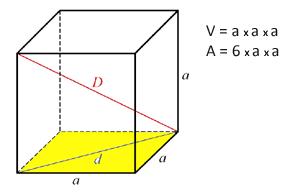 A kocka területe A kocka területe
Hogyan kell kiszámítani a kocka területét?
A terület kiszámítása: egy négyzet területe (oldaltól négyzetig - a2), és megszorozzuk 6-tal.
A = 6*a2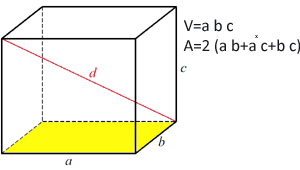 A téglalap alakú paralelepipedon térfogata A téglalap alakú paralelepipedon térfogata
A téglalap alakú paralelepipedon térfogatát úgy számítjuk ki, hogy az alap területét megszorozzuk a paralelepipedon magasságával
Térfogat képlete:
V=a*b*c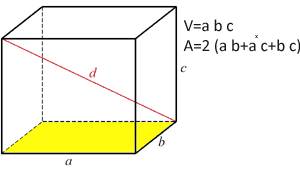 A téglalap alakú paralelepipedon területe A téglalap alakú paralelepipedon területe
A téglalap alakú paralelepipedon teljes területe 2* (ab oldal területe + ac oldal területe + bc oldal területe)
Az ab oldal területe = a x b
ac oldal területe = a x c
Oldalterület bc = b x c
Lapos geometria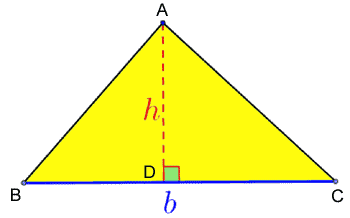 A háromszög területe A háromszög területe
Definíció szerint a háromszög területe b * h osztva 2-vel, ahol b az oldal hosszát, h pedig az oldalnak megfelelő magasság hosszát jelenti.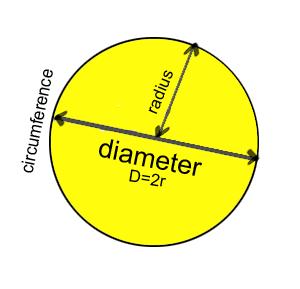 A kör átmérője és kerülete A kör átmérője és kerülete
Képlet
Átmérő d = 2 × r
Kerület C = π × d = 2 × π × r
A körtárcsa területe A = π × d²/4 = π × r²
π = 3,14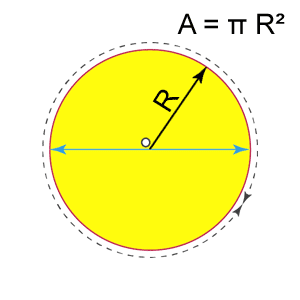 A kör területe A kör területe
Ha a kör sugara R, akkor a terület π R²
A=πR²
A kör területe egyenlő pi (π) szorozva a sugár négyzetével.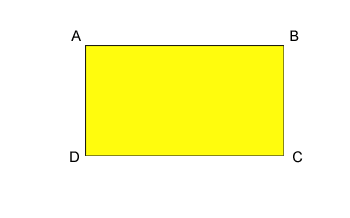 A téglalap kerülete A téglalap kerülete
A téglalap kerülete a téglalap 4 oldalának összege
P=AB+BC+CD+DA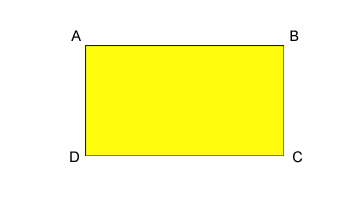 A téglalap területe A téglalap területe
A területet úgy számítjuk ki, hogy a hosszú oldalt megszorozzuk a rövid oldallal
A = AB x BC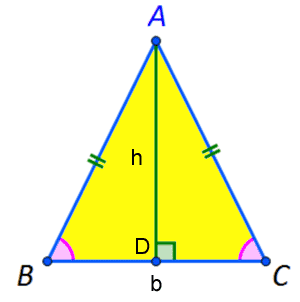 Az egyenlő szárú háromszög területe Az egyenlő szárú háromszög területe
Terület = (b*ó)/2
A terület egyenlő a (b) alap szorzatával (h) osztva 2-vel
A magasságot a Pitagorasz-tétel határozza meg abból a derékszögű háromszögből, amely akkor keletkezik, amikor a magasság az alapra merőlegesen esik Az ellipszis területe Az ellipszis területe
Definíció szerint az ellipszis területe egyenlő π × a × b, ahol a, b a féltengelyek, és π (pi) egy matematikai állandó, amely egyenlő 3,14159-cel.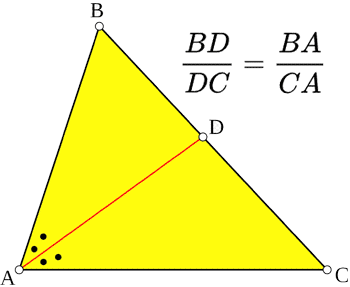 Felezőtétel Felezőtétel
Az ABC háromszögben az A szögfelező a szemközti oldalon (BC) a BD/DC=BA/CA szög oldalaival arányos szakaszokat határoz meg.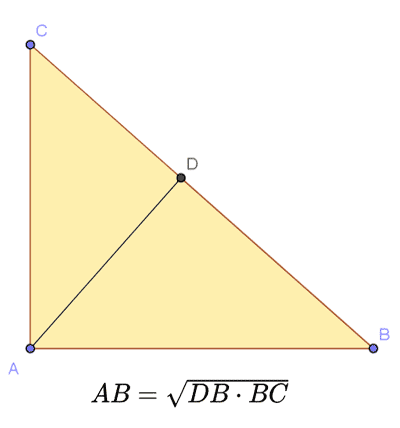 Lábtételt a következőképpen Lábtételt a következőképpen
Egy derékszögű háromszögben a láb hossza a befogói vetülete és a befogó hossza közötti geometriai átlag.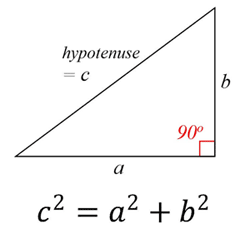 Pitagorasz tétel Pitagorasz tétel
A Pitagorasz-tétel kimondja, hogy bármely derékszögű háromszögben a lábak négyzeteinek összege egyenlő a befogó négyzetével (a derékszöggel ellentétes oldal).
Pythagoras kapcsolat:
a2 + b2 = c2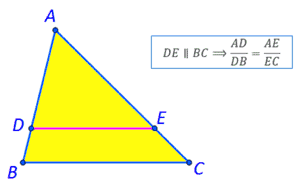 Thalész tétele Thalész tétele
A háromszög egyik oldalával párhuzamosan a másik két oldalon, vagy azok kiterjesztésein arányos szakaszok határozhatók meg.
Trigonometria Koszinusz - cos(x) - koszinusz függvény Koszinusz - cos(x) - koszinusz függvény
A koszinuszfüggvényt derékszögű háromszögben a szomszédos láb és a hipotenusz arányaként határozzuk meg. A függvény grafikonja koszinusz. A függvény -∞ és ∞ közötti intervallumban van definiálva, és -1 és 1 közötti értékei vannak. Szinusz sin(x) - szinuszfüggvény Szinusz sin(x) - szinuszfüggvény
Kiszámítja az eredményt Sine sin(x) a szinuszfüggvény
|