Algebra- Arytmetyka mediów
Formuła
ma = (x1+x2+ ... + xn) / n
Dacă a,b și c sunt numere reale, media aritmetică a acestora este ma = (a+b+c) / 3 - Oblicz procenty % Obliczanie procentów
Ile wynosi X % liczby Y?
Jak obliczyć procent liczby?
Można również zastosować prostą zasadę trzech - Ułamki zwykłe w ułamkach dziesiętnych – jak to zrobić?
Dowolny ułamek zwykły o potędze mianownika 10 można zapisać jako ułamek dziesiętny.
Jak zamienić ułamek zwykły na liczbę dziesiętną?
Naucz się zapisywać ułamki zwykłe w postaci dziesiętnej.
Jak przekonwertować system dziesiętny na binarny? - Zasada trzech
Prosta zasada trzech to metoda określania proporcjonalności.
Prosta zasada trzech części to metoda matematyczna, która pozwala na określenie jednego z warunków równania proporcjonalności na podstawie pozostałych.
Reguła powraca do obliczenia czwartej proporcjonalnej z proporcji:
a/b=c/x
Geometria w przestrzeni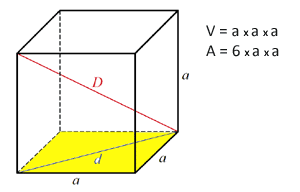 Objętość kostki Objętość kostki
Jak obliczyć objętość kostki?
Jaka jest formuła i figura.
Objętość jest równa powierzchni podstawy pomnożonej przez wysokość (bok kwadratu pomnożony przez a - a2*a)
V = a*a*a = a3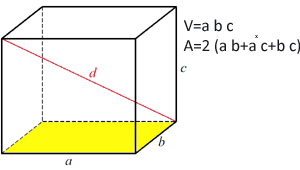 Objętość prostokątnego równoległościanu Objętość prostokątnego równoległościanu
Objętość równoległościanu prostokątnego oblicza się, mnożąc powierzchnię podstawy przez wysokość równoległościanu
Formuła objętości:
V=a*b*c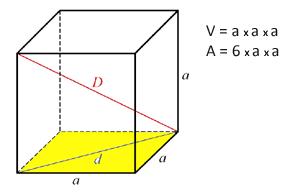 Powierzchnia kostki Powierzchnia kostki
Jak obliczyć powierzchnię kostki?
Powierzchnia jest obliczana: powierzchnia kwadratu (od boku do kwadratu - a2) i pomnożona przez 6.
A = 6*a2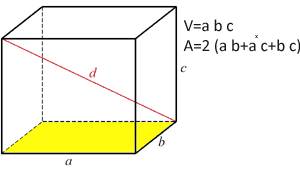 Powierzchnia prostokątnego równoległościanu Powierzchnia prostokątnego równoległościanu
Całkowita powierzchnia równoległościanu prostokątnego wynosi 2*(powierzchnia boku ab + powierzchnia boku ac + powierzchnia boku bc)
Powierzchnia boku ab = a x b
Powierzchnia boku ac = a x c
Powierzchnia boczna bc = b x c
Płaska geometria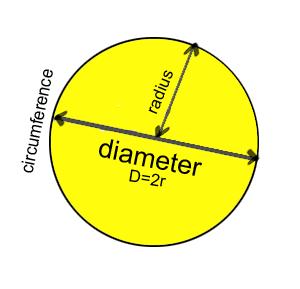 Średnica i obwód koła Średnica i obwód koła
Formuła
Średnica d = 2 × r
Obwód C = π × d = 2 × π × r
Powierzchnia tarczy kołowej A = π × d²/4 = π × r²
π = 3,14 Obszar elipsy Obszar elipsy
Z definicji pole elipsy jest równe π × a × b, gdzie a, b to półosie, a π (pi) to stała matematyczna równa 3,14159.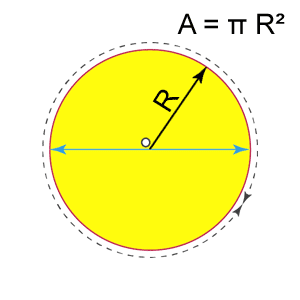 Obszar koła Obszar koła
Jeśli okrąg ma promień R, to pole wynosi π R²
A=πR²
Powierzchnia koła jest równa pi (π) pomnożonemu przez promień do kwadratu.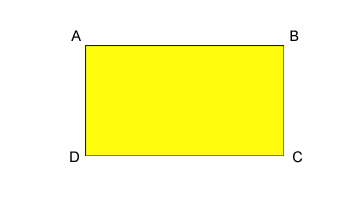 Obszar prostokąta Obszar prostokąta
Powierzchnia jest obliczana przez pomnożenie długiego boku przez krótki bok
A = AB x BC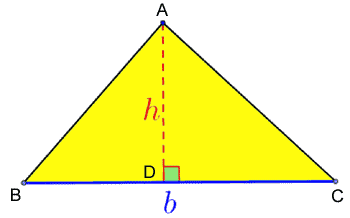 Obszar trójkąta Obszar trójkąta
Z definicji pole trójkąta to b * h podzielone przez 2, gdzie b oznacza długość boku, a h długość wysokości odpowiadającej temu bokowi.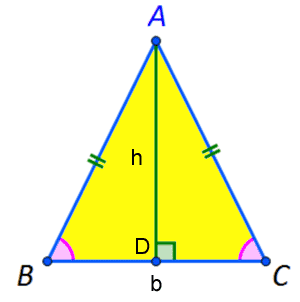 Obszar trójkąta równoramiennego Obszar trójkąta równoramiennego
Powierzchnia = (b*h)/2
Powierzchnia jest równa podstawie (b) pomnożonej przez wysokość (h) podzielonej przez 2
Wysokość znajduje się na podstawie twierdzenia Pitagorasa z trójkąta prostokątnego utworzonego, gdy wysokość spada prostopadle do podstawy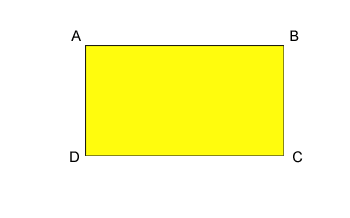 Obwód prostokąta Obwód prostokąta
Obwód prostokąta definiuje się jako sumę 4 boków prostokąta
P=AB+BC+CD+DA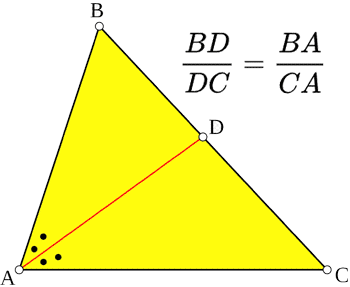 Twierdzenie o dwusiecznej Twierdzenie o dwusiecznej
W trójkącie ABC dwusieczna kąta A wyznacza po przeciwnej stronie (BC) odcinki proporcjonalne do boków kąta BD/DC=BA/CA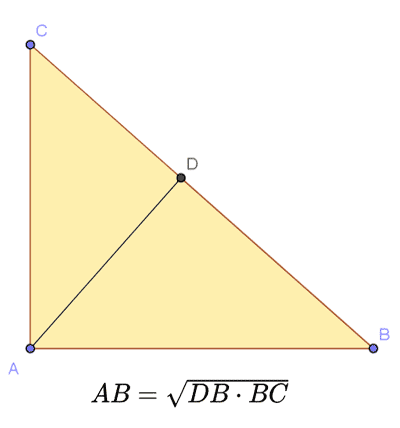 Twierdzenie o nodze i przeciwprostokątnej Twierdzenie o nodze i przeciwprostokątnej
W trójkącie prostokątnym długość nogi jest średnią geometryczną między długością jej rzutu na przeciwprostokątną a długością przeciwprostokątnej.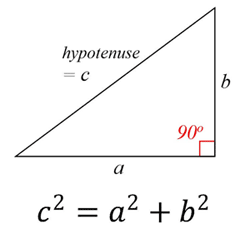 Twierdzenie Pitagorasa Twierdzenie Pitagorasa
Twierdzenie Pitagorasa mówi, że w każdym trójkącie prostokątnym suma kwadratów nóg jest równa kwadratowi przeciwprostokątnej (boku przeciwległemu do kąta prostego).
Relacja Pitagorasa:
a2 + b2 = c2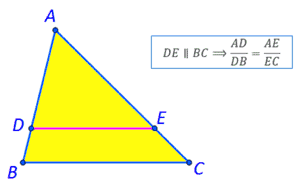 Twierdzenie Talesa Twierdzenie Talesa
Równolegle do jednego z boków trójkąta wyznacza na pozostałych dwóch bokach lub na ich przedłużeniach odcinki proporcjonalne.
Trygonometria Cosinus - cos(x) - funkcja cosinus Cosinus - cos(x) - funkcja cosinus
Funkcja cosinus jest zdefiniowana w trójkącie prostokątnym jako stosunek sąsiedniej nogi do przeciwprostokątnej. Wykres funkcji jest cosinusem. Funkcja jest zdefiniowana w przedziale od -∞ do ∞ i ma wartości od -1 do 1. Sinus sin(x) - funkcja sinus Sinus sin(x) - funkcja sinus
Oblicza wynik Sine sin(x) - funkcja sinus
|