CebirDüz geometri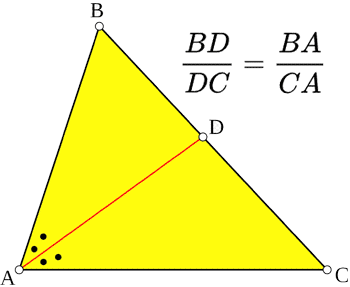 Açıortay teoremi Açıortay teoremi
Bir ABC üçgeninde, A açıortayı, karşı tarafta (BC) BD/DC=BA/CA açısının kenarlarıyla orantılı doğru parçaları belirler.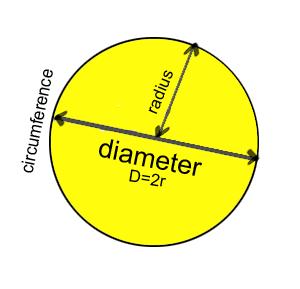 Çemberin çapı ve çevresi Çemberin çapı ve çevresi
formül
çap d = 2 × r
Çevre C = π × d = 2 × π × r
Dairesel diskin alanı A = π × d²/4 = π × r²
π = 3.14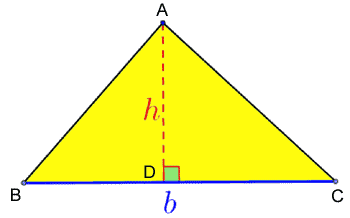 üçgenin alanı üçgenin alanı
Tanım olarak, bir üçgenin alanı b * h bölü 2'dir, burada b bir kenarın uzunluğunu ve h o kenara karşılık gelen yüksekliğin uzunluğunu temsil eder.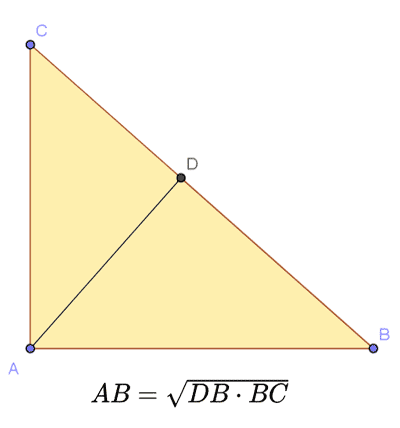 Bacak teoremi Bacak teoremi
Bir dik üçgende bir bacağın uzunluğu, hipotenüs üzerindeki çıkıntısının uzunluğu ile hipotenüsün uzunluğu arasındaki geometrik ortalamadır.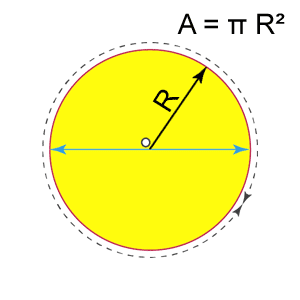 Dairenin alanı Dairenin alanı
Çemberin yarıçapı R ise, alan π R²'dir.
A=πR²
Bir dairenin alanı, yarıçapın karesi ile çarpılan pi (π) değerine eşittir.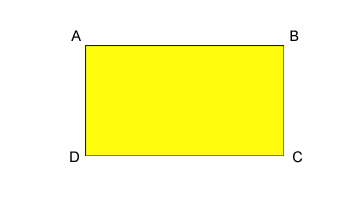 Dikdörtgenin alanı Dikdörtgenin alanı
Alan, uzun kenar ile kısa kenar çarpılarak hesaplanır.
A = AB x BC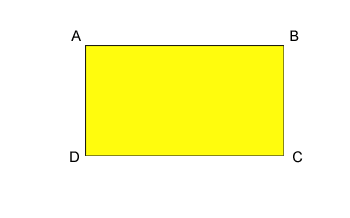 Dikdörtgenin çevresi Dikdörtgenin çevresi
Dikdörtgenin çevresi, dikdörtgenin 4 kenarının toplamı olarak tanımlanır
P=AB+BC+CD+DA Elipsin alanı Elipsin alanı
Tanım olarak elipsin alanı π × a × b'ye eşittir; burada a, b yarı eksenlerdir ve π (pi) 3.14159'a eşit bir matematiksel sabittir.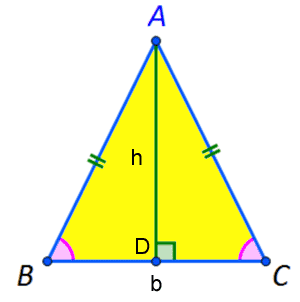 ikizkenar üçgenin alanı ikizkenar üçgenin alanı
Alan = (b*h)/2
Alan, taban (b) çarpı yükseklik (h) bölü 2'ye eşittir.
Pisagor teoremine göre yükseklik tabana dik düştüğünde oluşan dik üçgenden bulunur.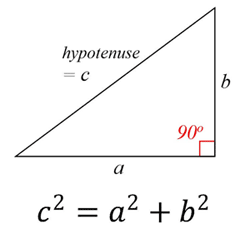 Pisagor Teoremi, Pisagor Teoremi Pisagor Teoremi, Pisagor Teoremi
Pisagor teoremi, herhangi bir dik üçgende, bacakların karelerinin toplamının hipotenüsün (dik açının karşısındaki kenar) karesine eşit olduğunu belirtir.
Pisagor ilişkisi:
a2 + b2 = c2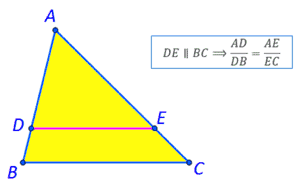 Thales teoremi Thales teoremi
Bir üçgenin kenarlarından birine paralel, diğer iki kenarda veya uzantılarında orantılı doğru parçaları belirler.
Trigonometri Kosinüs - cos(x) - kosinüs fonksiyonu Kosinüs - cos(x) - kosinüs fonksiyonu
Kosinüs işlevi, bir dik üçgende bitişik bacak ile hipotenüs arasındaki oran olarak tanımlanır. Fonksiyonun grafiği bir kosinüstür. Fonksiyon -∞ ile ∞ arasındaki aralıkta tanımlanır ve -1 ile 1 arasında değerlere sahiptir. sinüs sin(x) - sinüs işlevi sinüs sin(x) - sinüs işlevi
Sonucu hesaplar Sinüs sin(x) - sinüs fonksiyonu
Uzayda geometri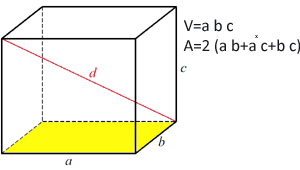 Dikdörtgen paralelkenarın hacmi Dikdörtgen paralelkenarın hacmi
Dikdörtgen paralel borunun hacmi, taban alanı ile paralel borunun yüksekliği çarpılarak hesaplanır.
Hacim formülü:
V=a*b*c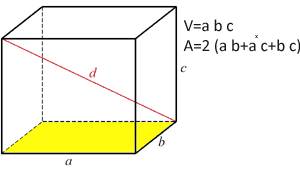 Dikdörtgen paralelyüzün alanı Dikdörtgen paralelyüzün alanı
Dikdörtgen paralel yüzün toplam alanı 2*(ab kenarının alanı + ac kenarının alanı + bc kenarının alanı)
Ab kenarının alanı = a x b
Yan alan ac = a x c
Yan alan bc = b x c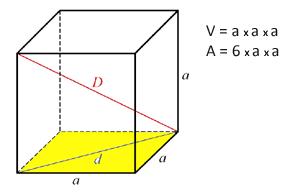 küpün alanı küpün alanı
Küpün alanı nasıl hesaplanır?
Alan hesaplanır: bir karenin alanı (kenardan kareye - a2) ve 6 ile çarpın.
A = 6*a2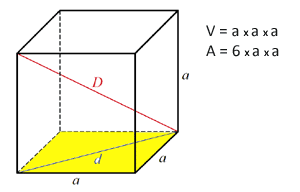 Küpün hacmi Küpün hacmi
Küpün hacmi nasıl hesaplanır?
Formül ve şekil nedir?
Hacim, taban alanı ile yüksekliğin çarpımına eşittir (kare çarpı a - a2*a)
V = a*a*a = a3
|