Algebra- Aritmetický průměr
Vzorec
ma = (x1+x2+ ... + xn) / n
Jsou-li a, b a c reálná čísla, jejich aritmetický průměr je ma = (a+b+c) / 3 - Pravidlo tří
Jednoduché pravidlo tří je metodou pro určení proporcionality.
Jednoduché pravidlo třetin je matematická metoda, která umoňuje určit jeden z členů rovnice proporcionality na základě ostatních.
Pravidlo se vrátí a vypočítá čtvrtou proporcionální část z proporcí:
a/b=c/x - Vypočítat procento % Výpočet procent
Kolik je X % čísla Y?
Jak vypočítat procento z čísla?
Lze pouít i jednoduché pravidlo tří - Zlomky v desetinných číslech – jak je provedu?
Jakýkoli běžný zlomek s mocninou jmenovatele 10 lze zapsat jako desetinný zlomek.
Jak mohu převést zlomek na desetinné číslo?
Naučte se psát obyčejné zlomky v desítkovém tvaru.
Jak převedu z desítkové soustavy na binární?
Geometrie v prostoru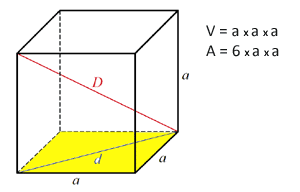 Objem krychle Objem krychle
Jak vypočítat objem krychle?
Jaký je vzorec a obrázek.
Objem se rovná ploe základny vynásobené výkou (druhá strana vynásobená a - a2*a)
V = a*a*a = a3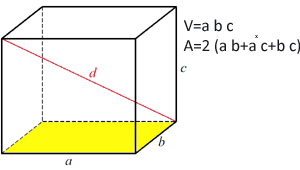 Objem pravoúhlého rovnoběnostěnu Objem pravoúhlého rovnoběnostěnu
Objem obdélníkového rovnoběnostěnu se vypočítá vynásobením plochy základny výkou rovnoběnostěnu
Objemový vzorec:
V=a*b*c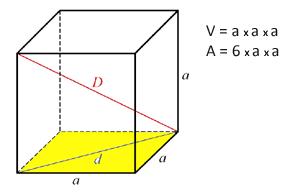 Plocha krychle Plocha krychle
Jak vypočítat plochu krychle?
Plocha se vypočítá: plocha čtverce (od strany ke čtverci - a2) a vynásobí se 6.
A = 6*a2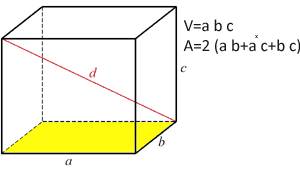 Plocha pravoúhlého rovnoběnostěnu Plocha pravoúhlého rovnoběnostěnu
Celková plocha pravoúhlého rovnoběnostěnu je 2* (plocha strany ab + plocha strany ac + plocha strany bc)
Plocha strany ab = a x b
Plocha strany ac = a x c
Boční plocha bc = b x c
Plochá geometrie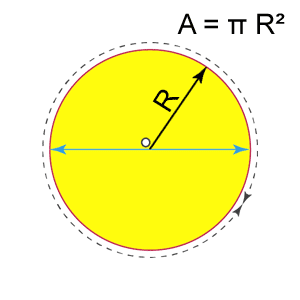 Oblast kruhu Oblast kruhu
Pokud má kruh poloměr R, pak je plocha π R²
A = πR²
Plocha kruhu se rovná pi (π) násobeném poloměrem na druhou.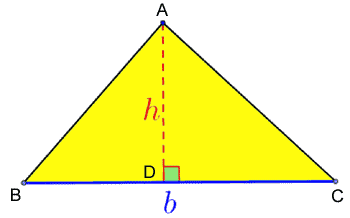 Oblast trojúhelníku Oblast trojúhelníku
Podle definice je plocha trojúhelníku b * h děleno 2, kde b představuje délku strany a h délku výky odpovídající této straně.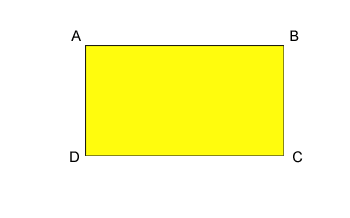 Obvod obdélníku Obvod obdélníku
Obvod obdélníku je definován jako součet 4 stran obdélníku
P=AB+BC+CD+DA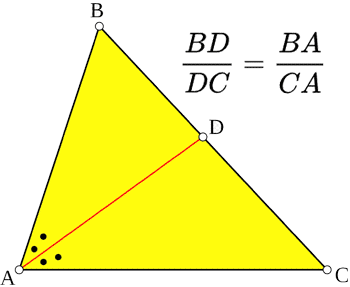 Osová věta Osová věta
V trojúhelníku ABC určuje úsečka A na opačné straně (BC) úsečky úměrné stranám úhlu BD/DC=BA/CA Plocha elipsy Plocha elipsy
Podle definice je plocha elipsy rovna π × a × b, kde a, b jsou poloosy a π (pi) je matematická konstanta rovna 3,14159.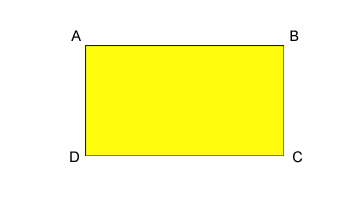 Plocha obdélníku Plocha obdélníku
Plocha se vypočítá vynásobením dlouhé strany krátkou stranou
A = AB x BC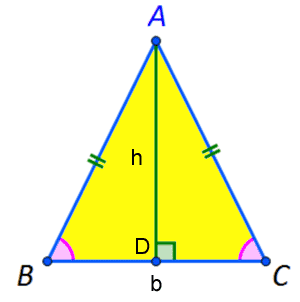 Plocha rovnoramenného trojúhelníku Plocha rovnoramenného trojúhelníku
Plocha = (b*h)/2
Plocha se rovná základně (b) vynásobené výkou (h) dělenou 2
Výku zjistíme pomocí Pythagorovy věty z pravoúhlého trojúhelníku vytvořeného, kdy výka klesne kolmo k základně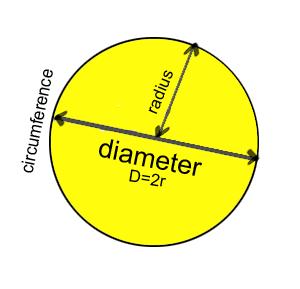 Průměr a obvod kruhu Průměr a obvod kruhu
Vzorec
Průměr d = 2 × r
Obvod C = π × d = 2 × π × r
Plocha kruhového disku A = π × d²/4 = π × r²
π = 3,14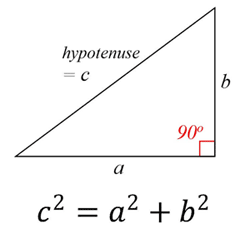 Pythagorova věta Pythagorova věta
Pythagorova věta říká, e v kadém pravoúhlém trojúhelníku je součet čtverců nohou roven čtverci přepony (strana protilehlá pravému úhlu).
Pythagorův vztah:
a2 + b2 = c2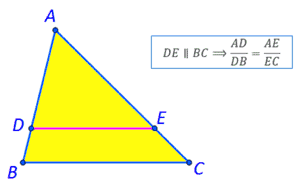 Thalesova věta Thalesova věta
Rovnoběka k jedné ze stran trojúhelníku určuje na dalích dvou stranách nebo na jejich prodloueních proporcionální úsečky.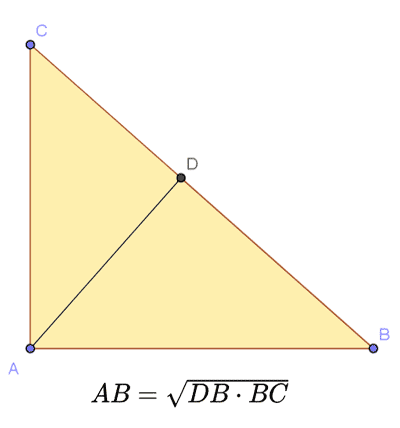 Věta o noze Věta o noze
V pravoúhlém trojúhelníku je délka nohy geometrickým průměrem mezi délkou jejího průmětu na přeponu a délkou přepony.
Trigonometrie |